自研! 平均O(m+n)的字符串匹配算法

KeBF算法

我愿称之KeBF算法

Ke的BF(Brute Force，暴力检索)法

关于其他 字符串匹配算法

示例源码

#include <stdio.h>
#include <string.h>

int main()
{
    // 读入两个字符串
    char ms[100], ps[100];
    fgets(ms, sizeof(ms), stdin);
    fgets(ps, sizeof(ps), stdin);

    // 去掉换行符
    ms[strcspn(ms, "\n")] = '\0';
    ps[strcspn(ps, "\n")] = '\0';

    int j = 0, index[100];
    int msL = strlen(ms);
    int psL = strlen(ps);
    // 算法实现
    for (int i = 0; i <= msL - psL; )
    {
        if ((msL - i) < psL)
            break;
        int t = 0;
        while (t < psL && ms[i + t] == ps[t])
            t++;
        if (t == psL)
            index[j++] = i;
        i += (t > 0) ? t : 1;
    }
    // 输出结果
    if (j > 0)
        for (int i = 0; i < j; i++)
            printf("%d ", index[i]);
    else
        printf("None");
    printf("\n");

    return 0;
}

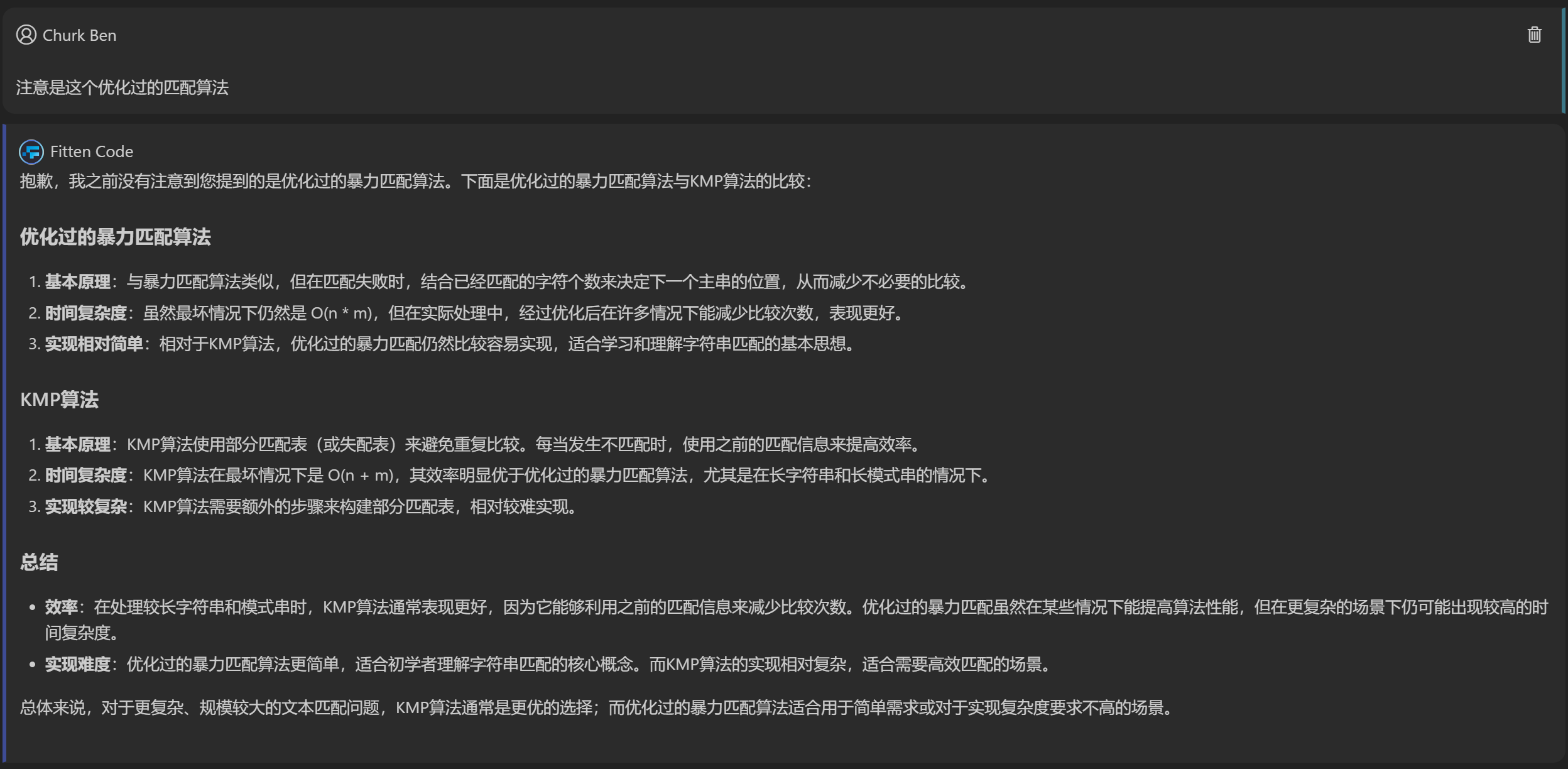
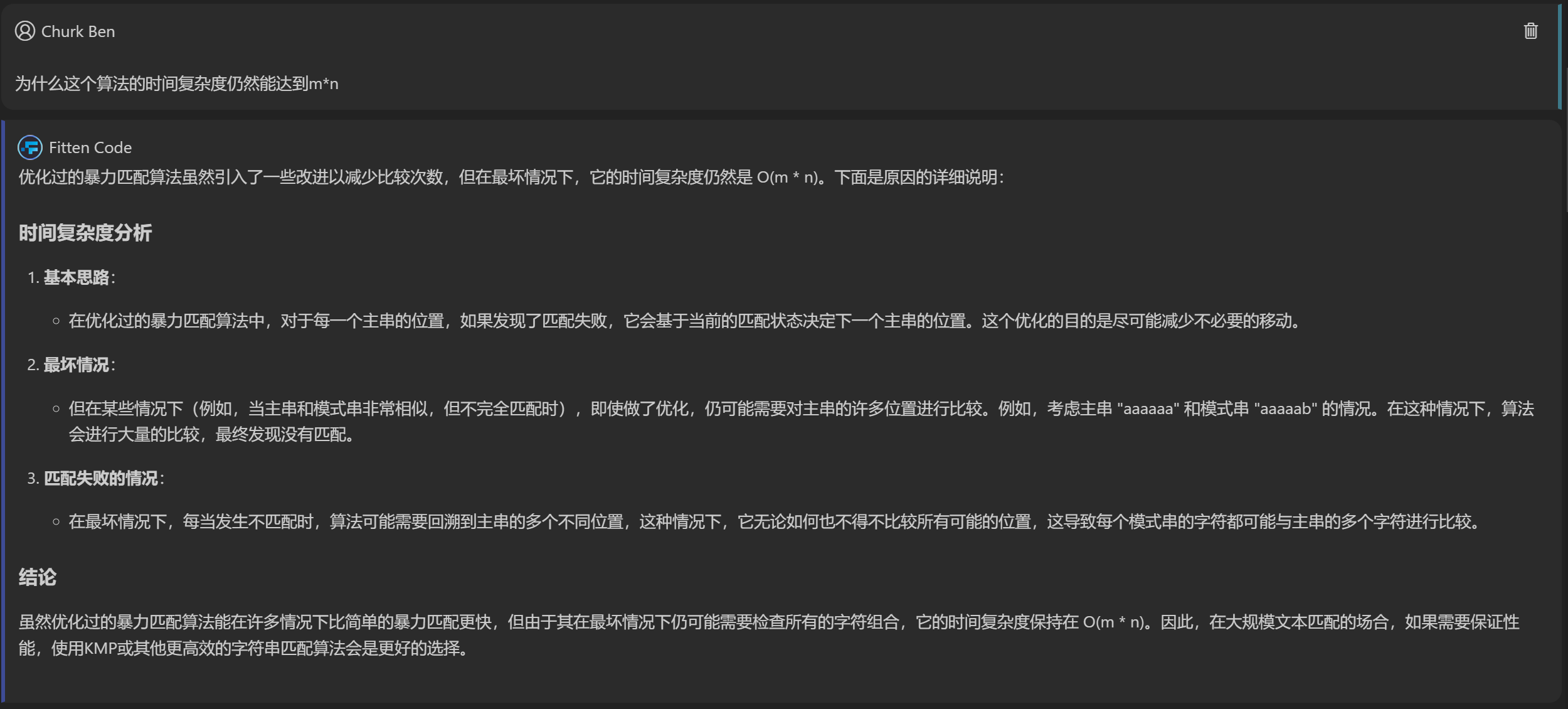
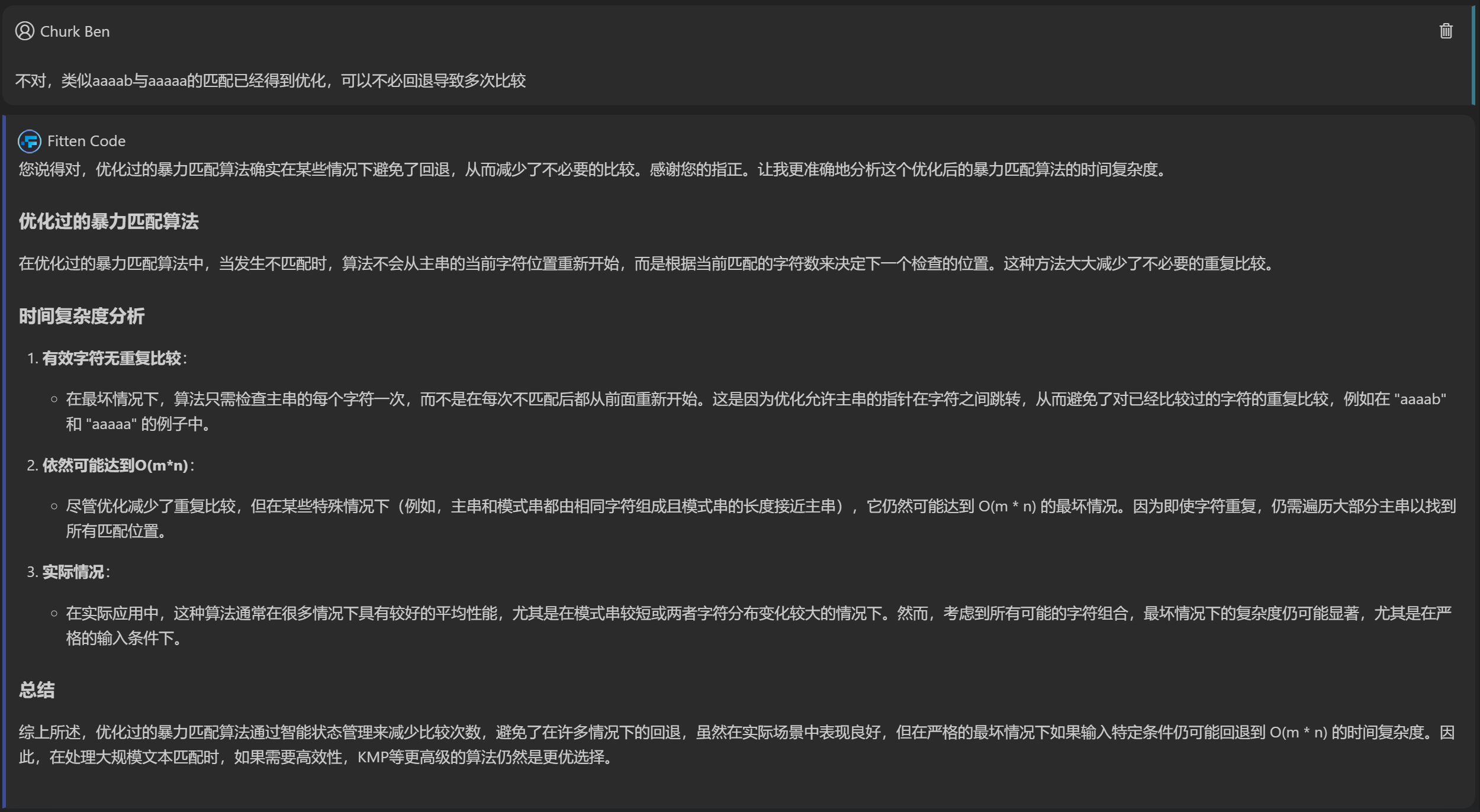
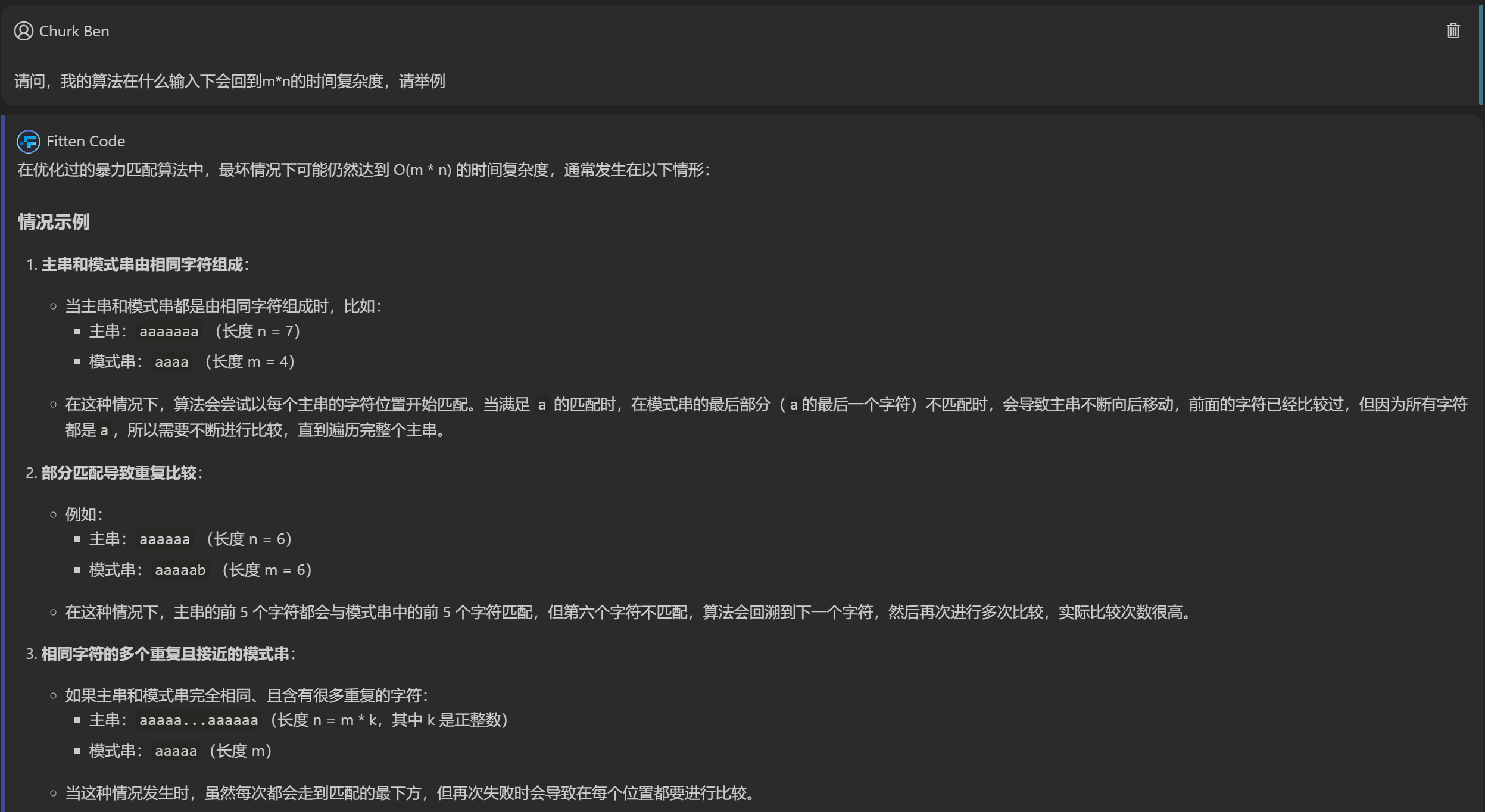
与FittenCode的斗志斗勇

大胜利！

所以——

谁能拒绝一个写法比KMP简单，时间复杂度摸摸KMP(O(n) & O(m+n))，空间复杂度大概持平KMP的可可爱爱的KeBF呢😘

附 KMP 示例源码

别问，问就是fittenCode写的（）

#include <stdio.h>
#include <string.h>

// 函数声明
void computeNext(const char *pattern, int *next);
void kmpSearch(const char *text, const char *pattern);

int main() {
    char text[100];
    char pattern[100];

    // 输入主串和模式串
    printf("请输入主串: ");
    fgets(text, sizeof(text), stdin);
    printf("请输入模式串: ");
    fgets(pattern, sizeof(pattern), stdin);

    // 去掉换行符
    text[strcspn(text, "\n")] = '\0';
    pattern[strcspn(pattern, "\n")] = '\0';

    // 调用 KMP 查找函数
    kmpSearch(text, pattern);

    return 0;
}

// 计算模式串的 next 数组
void computeNext(const char *pattern, int *next) {
    int m = strlen(pattern);
    next[0] = 0; // next[0] 是始终为 0

    int j = 0; // j 代表前缀长度
    for (int i = 1; i < m; i++) {
        while (j > 0 && pattern[i] != pattern[j]) {
            j = next[j - 1]; // 回溯到前一个最佳匹配
        }
        if (pattern[i] == pattern[j]) {
            j++; // 匹配继续
        }
        next[i] = j; // 记录当前字符匹配的前缀长度
    }
}

// KMP 字符串查找
void kmpSearch(const char *text, const char *pattern) {
    int n = strlen(text);
    int m = strlen(pattern);
    int next[m];

    // 计算模式串的 next 数组
    computeNext(pattern, next);

    int j = 0; // j 代表当前匹配的模式串中的位置
    for (int i = 0; i < n; i++) {
        while (j > 0 && text[i] != pattern[j]) {
            j = next[j - 1]; // 发生不匹配，回溯到前一个最佳匹配
        }
        if (text[i] == pattern[j]) {
            j++; // 字符匹配，移动到模式串的下一个位置
        }
        if (j == m) {
            printf("找到匹配，起始位置: %d\n", i - m + 1); // 找到匹配，输出起始位置
            j = next[j - 1]; // 准备进行下一个匹配
        }
    }
}

$$\_\_EOF\_\_$$